What is Counting Sort Algorithm?
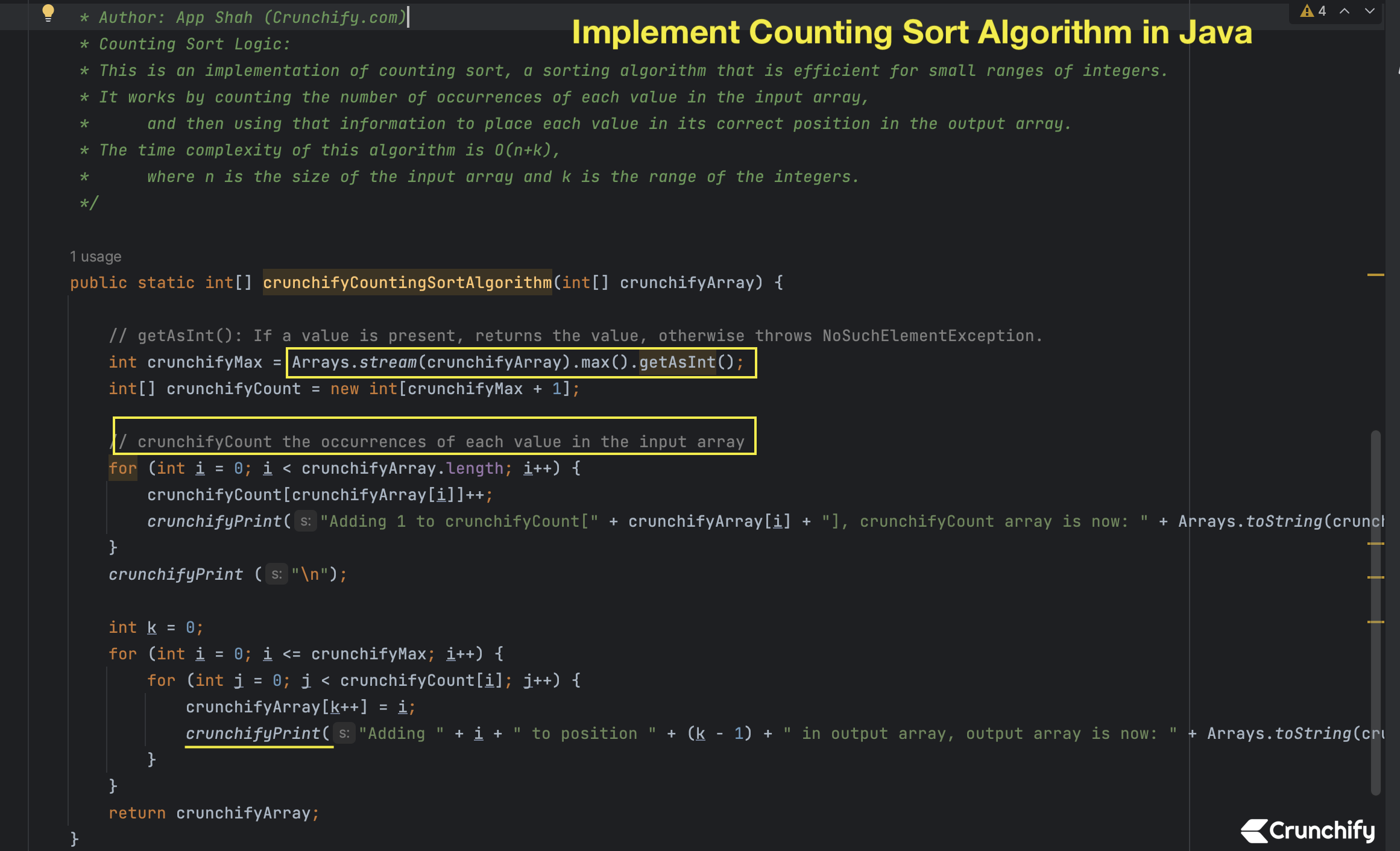
Counting sort, a sorting algorithm that is efficient for small ranges of integers. It works by counting the number of occurrences of each value in the input array, and then using that information to place each value in its correct position in the output array.
The time complexity of this algorithm is O(n+k), where n is the size of the input array and k is the range of the integers.
CrunchifyCountingSortAlgo.java
Here is a complete implementation of Counting Sort in Java. Just copy it into your preferred IDEA and run it.
package crunchify.com.java.tutorials;
import java.util.Arrays;
/**
* @author Crunchify.com
* Program: How to implement Counting sort algorithm in java?
* Counting sort is a sorting algorithm that sorts the elements of an array
* by counting the number of occurrences of each unique element in the array.
*/
public class CrunchifyCountingSortAlgo {
public static void main(String[] args) {
// Integer Array of 10 elements
int[] crunchifyArray = {9, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3};
crunchifyPrint("Original Array: " + Arrays.toString(crunchifyArray));
crunchifyPrint ("\n");
CrunchifyCountingSortAlgo crunchify = new CrunchifyCountingSortAlgo();
crunchify.crunchifyCountingSortAlgorithm(crunchifyArray);
crunchifyPrint ("\n");
crunchifyPrint("Result of Crunchify Counting Sort Algorithm: " + Arrays.toString(crunchifyArray));
}
private static void crunchifyPrint(String s) {
System.out.println(s);
}
/**
* Author: App Shah (Crunchify.com)
*
* Counting Sort Logic:
* This is an implementation of counting sort, a sorting algorithm that is efficient for small ranges of integers.
* It works by counting the number of occurrences of each value in the input array,
* and then using that information to place each value in its correct position in the output array.
* The time complexity of this algorithm is O(n+k),
* where n is the size of the input array and k is the range of the integers.
*/
public static int[] crunchifyCountingSortAlgorithm(int[] crunchifyArray) {
// getAsInt(): If a value is present, returns the value, otherwise throws NoSuchElementException.
int crunchifyMax = Arrays.stream(crunchifyArray).max().getAsInt();
int[] crunchifyCount = new int[crunchifyMax + 1];
// crunchifyCount the occurrences of each value in the input array
for (int i = 0; i < crunchifyArray.length; i++) {
crunchifyCount[crunchifyArray[i]]++;
crunchifyPrint("Adding 1 to crunchifyCount[" + crunchifyArray[i]
+ "], crunchifyCount array is now: " + Arrays.toString(crunchifyCount));
}
crunchifyPrint ("\n");
int k = 0;
for (int i = 0; i <= crunchifyMax; i++) {
for (int j = 0; j < crunchifyCount[i]; j++) {
crunchifyArray[k++] = i;
crunchifyPrint("Adding " + i + " to position " + (k - 1)
+ " in output array, output array is now: " + Arrays.toString(crunchifyArray));
}
}
return crunchifyArray;
}
}
Just run above program as a Java Application in IntelliJ IDEA or Eclipse IDE and you will result as below.
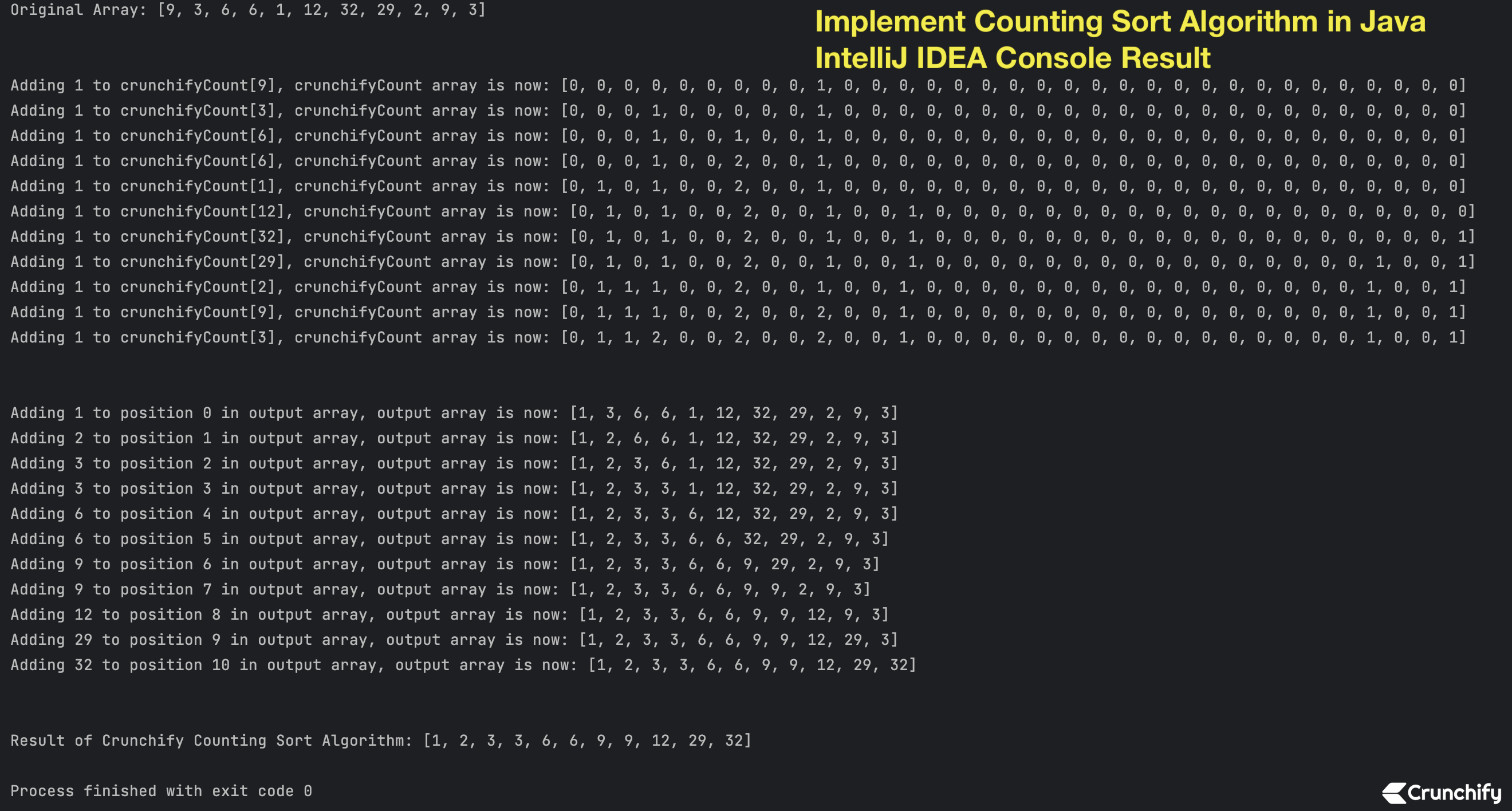
IntelliJ IDEA Console Result
Original Array: [9, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3] Adding 1 to crunchifyCount[9], crunchifyCount array is now: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Adding 1 to crunchifyCount[3], crunchifyCount array is now: [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Adding 1 to crunchifyCount[6], crunchifyCount array is now: [0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Adding 1 to crunchifyCount[6], crunchifyCount array is now: [0, 0, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Adding 1 to crunchifyCount[1], crunchifyCount array is now: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Adding 1 to crunchifyCount[12], crunchifyCount array is now: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] Adding 1 to crunchifyCount[32], crunchifyCount array is now: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1] Adding 1 to crunchifyCount[29], crunchifyCount array is now: [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1] Adding 1 to crunchifyCount[2], crunchifyCount array is now: [0, 1, 1, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1] Adding 1 to crunchifyCount[9], crunchifyCount array is now: [0, 1, 1, 1, 0, 0, 2, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1] Adding 1 to crunchifyCount[3], crunchifyCount array is now: [0, 1, 1, 2, 0, 0, 2, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1] Adding 1 to position 0 in output array, output array is now: [1, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3] Adding 2 to position 1 in output array, output array is now: [1, 2, 6, 6, 1, 12, 32, 29, 2, 9, 3] Adding 3 to position 2 in output array, output array is now: [1, 2, 3, 6, 1, 12, 32, 29, 2, 9, 3] Adding 3 to position 3 in output array, output array is now: [1, 2, 3, 3, 1, 12, 32, 29, 2, 9, 3] Adding 6 to position 4 in output array, output array is now: [1, 2, 3, 3, 6, 12, 32, 29, 2, 9, 3] Adding 6 to position 5 in output array, output array is now: [1, 2, 3, 3, 6, 6, 32, 29, 2, 9, 3] Adding 9 to position 6 in output array, output array is now: [1, 2, 3, 3, 6, 6, 9, 29, 2, 9, 3] Adding 9 to position 7 in output array, output array is now: [1, 2, 3, 3, 6, 6, 9, 9, 2, 9, 3] Adding 12 to position 8 in output array, output array is now: [1, 2, 3, 3, 6, 6, 9, 9, 12, 9, 3] Adding 29 to position 9 in output array, output array is now: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 3] Adding 32 to position 10 in output array, output array is now: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 32] Result of Crunchify Counting Sort Algorithm: [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 32] Process finished with exit code 0
Let me know if you face any issue running above Counting Sort Algorithm Java program.
The post Implement Counting Sort Algorithm in Java appeared first on Crunchify.
0 Commentaires